1.两数之和(1)

暴力破解
我首先想到的是暴力破解,使用双循环,但这种方法时间复杂度太高,好在容易想到
class Solution(object):
def twoSum(self, nums, target):
for i in range(len(nums)):
for j in range(i+1 , len(nums)):
if nums[i] + nums[j] == target:
return[i,j]哈希法
在我理解里,这种做法很讨巧,先定义一个idx字典(用来存放索引值),然后对nums的元素进行枚举,判断target – x是否已经存放在idx里面,如果已经存在,就输出返回值,如果不存在就idx[x] = j将对应的数值以哈希方式存放
class Solution(object):
def twoSum(self, nums, target):
idx = {}
for j , x in enumerate(nums):
if target - x in idx:
return [idx[target - x], j]
idx[x] = j2.字母异位词分组(49)

刚看到这道题,由于我的算法见识过于浅薄,首先想到的还是使用暴力,但此处如果使用暴力应该会很麻烦,所以选择阅读题解,看到使用一种字符串排序的方式觉得很有意思,将strs数组里的字符串进行排序操作,最终异位词会以相同的形式呈现,此时只要将对应的形式进行分类,再将数组里的数字填入即可
class Solution:
def groupAnagrams(self, strs: List[str]) -> List[List[str]]:
d = defaultdict(list)
for s in strs:
sorted_s = ''.join(sorted(s))
d[sorted_s].append(s)
return list(d.values())3.最长连续序列(128)

刚看到这道题我的想法还是暴力(比较蠢),后来看题解选择使用了一种集合的思想,将原本的数组转化成集合,然后对其中的每一个数字判断集合里是否有比他小1的数字,如果有就去下一个数字,如果没有就判断是否有比他大1的数字,如果则长度加一
集合判断
class Solution:
def longestConsecutive(self, nums: List[int]) -> int:
st = set(nums)
ans = 0
for x in st:
if x - 1 in st:
continue
y = x + 1
while y in st:
y += 1
ans = max(ans, y - x)
return ans暴力破解
除了这种做法以外就是暴力了,先将数组排序,然后依次比较后一位是否只比前一位大一
class Solution:
def longestConsecutive(self, nums: List[int]) -> int:
nums.sort()
ans = 1
count = 1
if len(nums) == 0:
return 0
for i in range(len(nums) - 1):
if nums[i+1] - nums[i] == 1:
count += 1
ans = max(ans, count)
elif nums[i + 1] - nums[i] == 0:
continue
else:
count = 1
return ans4.移动零(283)

首先我想到的依旧是暴力,遍历数组然后出现零就把数字放到末尾,把后一位前移,但实际上看了题解之后发现了一个更好的方式:原地栈
原地栈
先设置栈大小为0,然后对数组所有元素进行判断,是否为0,如果不是,就放入栈中,然后栈指针后移1位,最后再把剩余部分用0补全,非常聪明
class Solution:
def moveZeroes(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
stack_size = 0
for x in nums:
if x:
nums[stack_size] = x
stack_size += 1
for i in range(stack_size, len(nums)):
nums[i] = 0快慢指针
另一种做法是快慢双指针,用fast指针去跑,slow指针用来更新元素,slow初始为零,如果fast碰到的元素非0,则将slow的位置更新成fast的元素,然后slow指针后移一位,同时把fast更新成slow更新前的元素
class Solution:
def moveZeroes(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
slow = 0
for fast in range(len(nums)):
if nums[fast]:
temp = nums[slow]
nums[slow] = nums[fast]
nums[fast] = temp
slow += 15.盛最多水的容器(11)
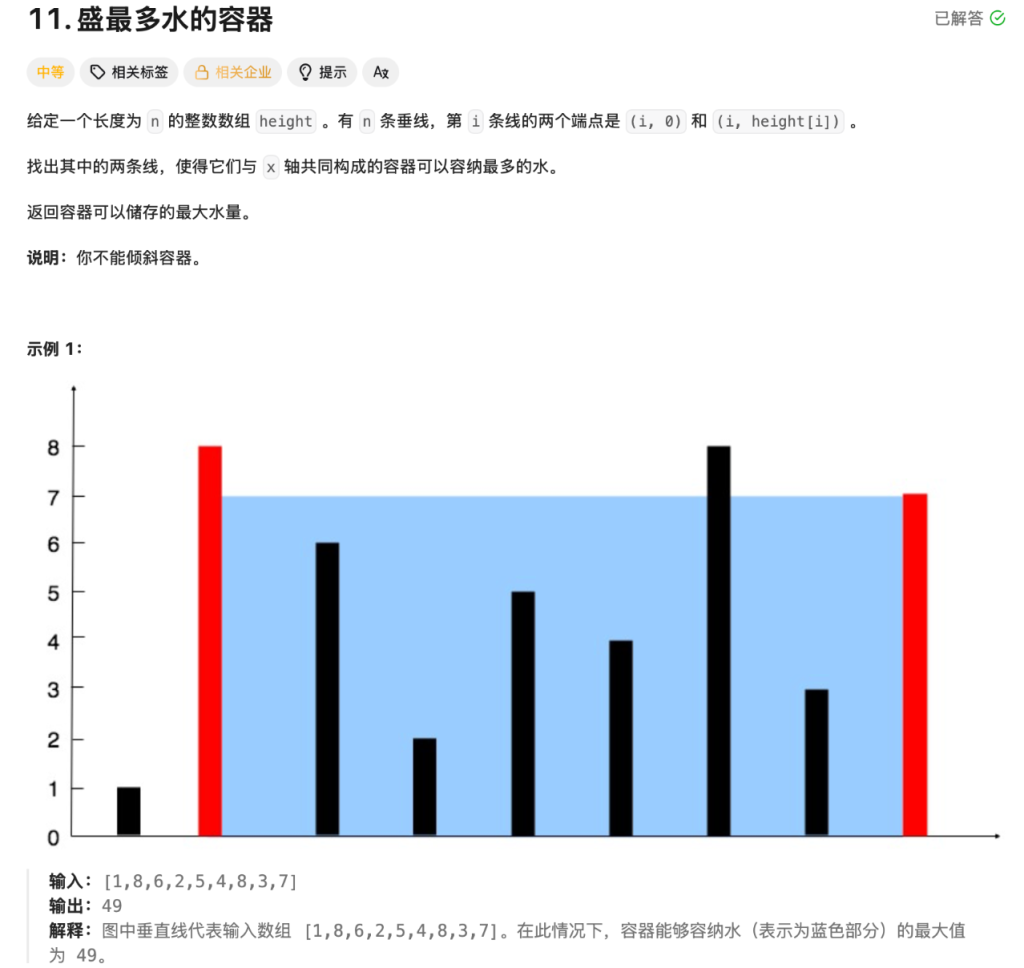
关于这道题我的思路比较简单,由于容纳水量的最大值有木桶效应,所以此时我们只需要考虑两块板子中最小的一块,然后以它的高度乘以两块板子的间距,之后把选择两块板子中较短一块的板子替换,同时用ans时刻更新最大值就可以
class Solution:
def maxArea(self, height: List[int]) -> int:
left = 0
right = len(height) - 1
ans = 0
while left < right:
ans = max(ans, min(height[left],height[right]) * (right - left))
if height[right] < height[left]:
right -= 1
else:
left += 1
return ans6.三数之和(15)
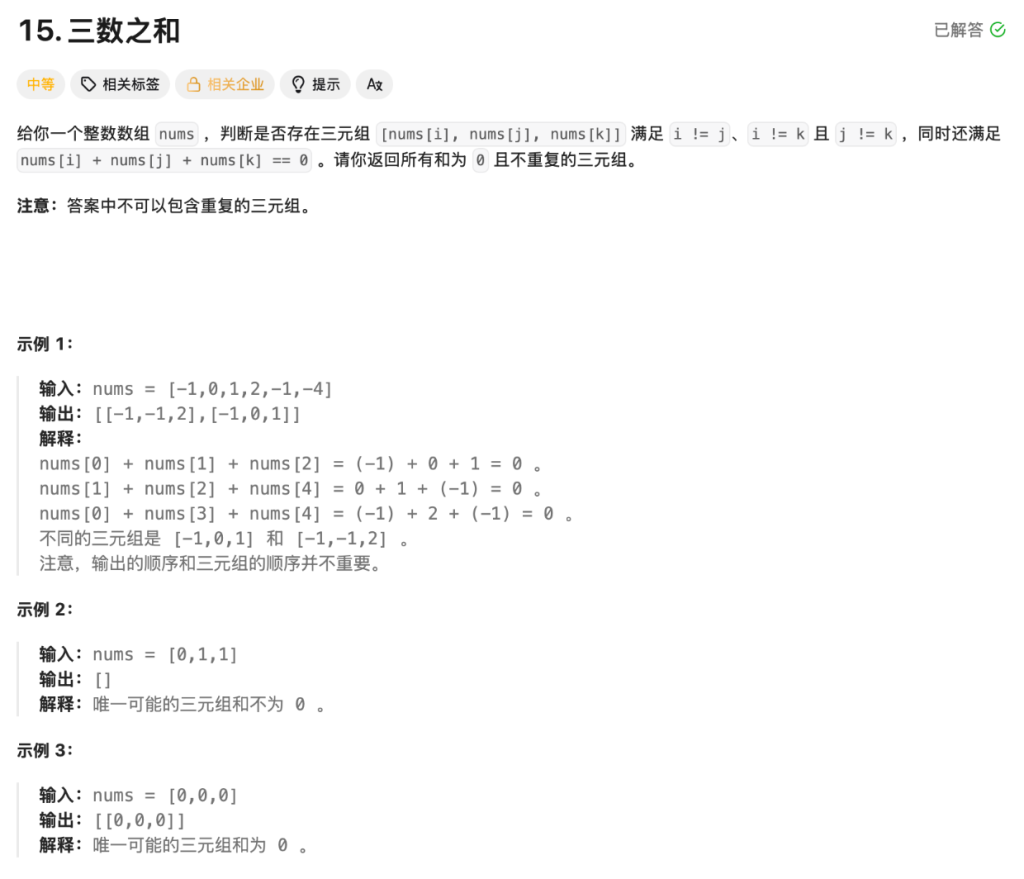
这道题的思路依然是学习来的,学了一种相向双指针的思路,这道题看似是三个数字之和为0,但实际上我们可以拆解成:假如说第一个数字已经确定了,那么我们就去控制后面两个数字,由于排序后的数字是有序的,我们可以根据三者之和s进行判断:
如果大于0,那么第三个数字过大,我们向前移一位
如果小于0,则第二个数字过小,往后移一位
之后,我们要考虑不要出现重复的情况,所以判断如果两个指针前后对应的数字相同,就continue继续找一位。
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
nums.sort()
ans = []
n = len(nums)
for i in range(n - 2):
x = nums[i]
if i > 0 and x == nums[i - 1]:
continue
if x + nums[i + 1] + nums[i + 2] > 0:
break
if x + nums[n-1] + nums[n - 2] < 0:
continue
j = i + 1
k = n - 1
while j < k:
s = x + nums[j] + nums[k]
if s > 0:
k -= 1
elif s < 0:
j += 1
else:
ans.append([x, nums[j], nums[k]])
j += 1
while j < k and nums[j] == nums[j - 1]:
j += 1
k -= 1
while j < k and nums[k] == nums[k + 1]:
k -= 1
return ans7.接雨水(42)

这道题两个月前做过,今天又做,除了双指针脑子里一点东西没有,关键双指针还没弄出来,最终又看了一遍视频,此刻想到两种做法
前缀后缀和
首先从头往后一次记录当前位置之前或者之后最高的位置,放入数组中进行记录,最终在求当前位置可盛水高度时,只需将前面最高和后面最高中的较低者,减去当前位置的高度就可以得出
class Solution:
def trap(self, height: List[int]) -> int:
n = len(height)
pre_max = [0] * n
pre_max[0] = height[0]
for i in range(1, n):
pre_max[i] = max(pre_max[i - 1], height[i])
suf_max = [0] * n
suf_max[-1] = height[-1]
for j in range(n - 2, -1, -1):
suf_max[j] = max(suf_max[j + 1], height[j])
ans = 0
for h, pre, suf in zip(height, pre_max, suf_max):
ans += min(pre, suf) - h
return ans相向双指针
思路和上一题大致相同,只不过此时我们使用相向双指针记录左边和右边的最大值
class Solution:
def trap(self, height: List[int]) -> int:
n = len(height)
ans = 0
pre_max = 0
suf_max = 0
left = 0
right = len(height) - 1
while left < right:
pre_max = max(pre_max, height[left])
suf_max = max(suf_max, height[right])
if pre_max < suf_max:
ans += pre_max - height[left]
left += 1
else:
ans += suf_max - height[right]
right -= 1
return ans8.无重复字符的最长字串(3)

这里需要注意一下,Python中有一个Counter()数组,自动记录数组中对应键的出现次数,这道题我们可以使用这个数组以哈希的方式来从前向后记录每个字符出现的次数,如果出现次数大于一就将做指针向后移一个,此处有使用到滑动窗口的思想
class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
cnt = Counter()
ans = 0
left = 0
if len(s) == 0:
return 0
for right, c in enumerate(s):
cnt[c] += 1
while cnt[c] > 1:
cnt[s[left]] -= 1
left += 1
ans = max(ans, right - left + 1)
return ans9.找到字符串中所有字母异位词(438)

这道题运用到的思想和上一题也很类似,哈希存储出现次数+滑动窗口。我们首先定义一个cnt_p来记录目标p字符串各个字符的出现次数作为标准,再定义cnt_s来记录被查字符串s的各个字符的出现次数。
使用滑动窗口,挨个字符向内加入,并时刻更新left指针位置,保证校验长度正常,然后时刻判断cnt_s 和cnt_p 是否一致,若一致则将left指针位置填入ans 数组当中
class Solution:
def findAnagrams(self, s: str, p: str) -> List[int]:
ans = []
cnt_p = Counter(p)
cnt_s = Counter()
right = 0
for right, c in enumerate(s):
cnt_s[c] += 1
left = right - len(p) + 1
if left < 0:
continue
if cnt_s == cnt_p:
ans.append(left)
out = s[left]
cnt_s[out] -= 1
if cnt_s[out] == 0:
del cnt_s[out]
return ans 10.和为K 的子数组(560)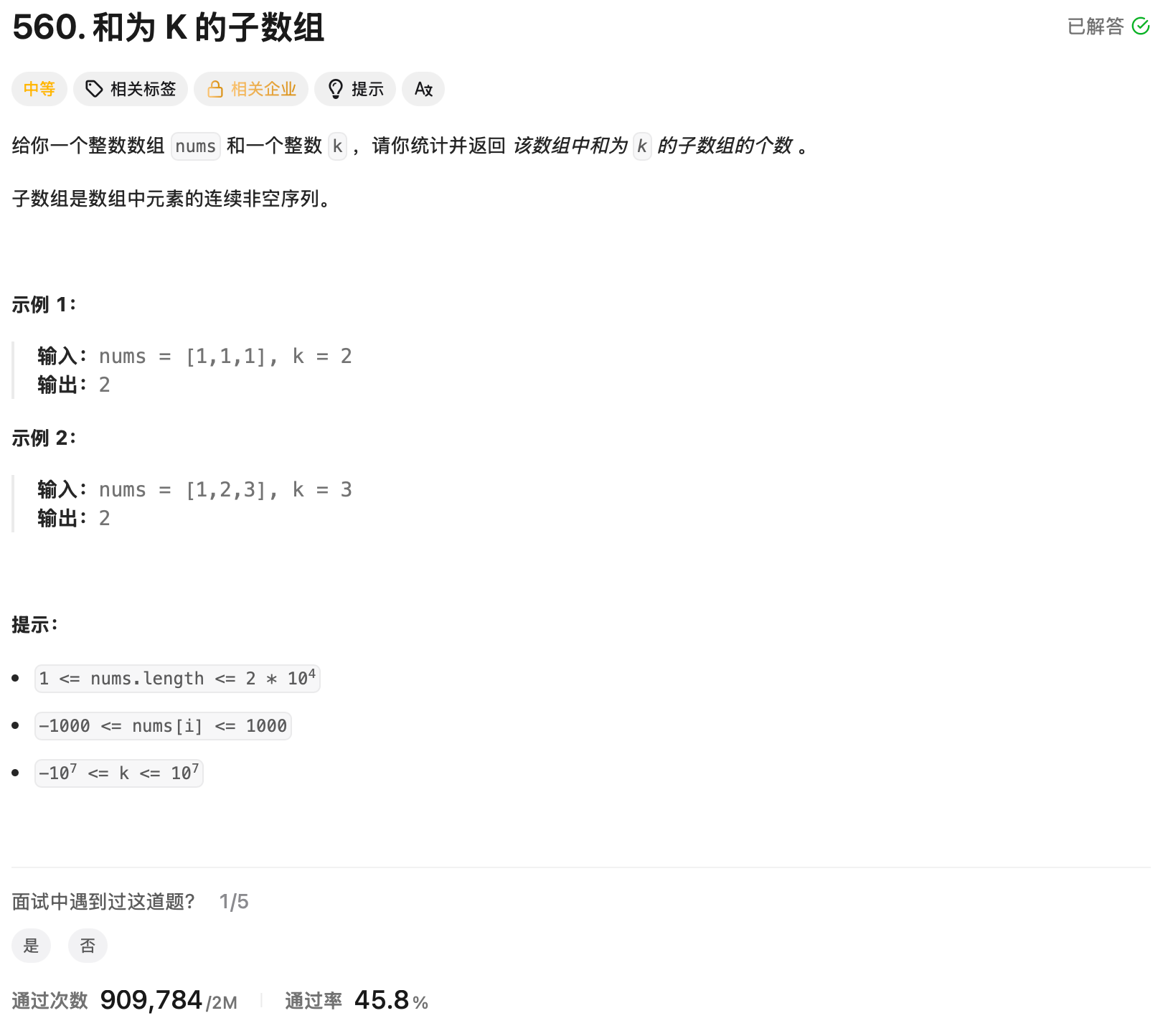

这道题使用前缀和求解,首先定义一个s数组长度为nums加一,然后将数组第一位置0,后续的全部用前缀和填入,再定义一个 cnt 用来记录 s 数组里每个前缀和的出现数量,我们可以得知,sj – k 的数值就是我们所需要的前缀和的大小,然后使用 ans 来记录这个值出现的次数,那么我们就可以算出有多少子数组满足条件
class Solution:
def subarraySum(self, nums: List[int], k: int) -> int:
s = [0] * (len(nums) + 1)
for i, x in enumerate(nums):
s[i + 1] = s[i] + x
cnt = defaultdict(int)
ans = 0
for sj in s:
ans += cnt[sj - k]
cnt[sj] += 1
return ans11.滑动窗口最大值(239)

刚看到这道题我的想法比较固定,还是用滑动窗口的思想来找出对应的最大值,先找到我需要操作的窗口然后在窗口里找到最大值,但实际上这样操作起来相对比较麻烦。
更聪明的做法是用一个双端队列实现,每次对新加入的数据进行判断,判断它是否比目前窗口内的最大数据大,如果更大就把旧数据弹出,加入新数据的下标,有新数据加入那么滑动窗口里最左端的数据就需要弹出,那么我们可以使用left = i – k + 1 来记录左端点的位置,如果窗口目前最大值的位置小于 left,那么将左端点弹出,顺便记录下对应的 ans 值
class Solution:
def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
ans = [0] * (len(nums) - k + 1) # 窗口个数
q = deque() # 双端队列
for i, x in enumerate(nums):
# 1. 右边入
while q and nums[q[-1]] <= x:
q.pop() # 维护 q 的单调性
q.append(i) # 注意保存的是下标,这样下面可以判断队首是否离开窗口
# 2. 左边出
left = i - k + 1 # 窗口左端点
if q[0] < left: # 队首离开窗口
q.popleft()
# 3. 在窗口左端点处记录答案
if left >= 0:
# 由于队首到队尾单调递减,所以窗口最大值就在队首
ans[left] = nums[q[0]]
return ans12.最小覆盖子串(76)

这道题的思想主要是用滑动窗口配合哈希表来记录对应字符的出现次数,那么我们只要便使用滑动窗口,边使用哈希表进行记录,如果cnt_s的值与cnt_t的值相等,那么说明我们目前已经找到了覆盖子串,同时我们再定义对应的left、right和ans_left、ans_right来记录找出最小的覆盖子串,最后输出的时候只要输出s[ans_left:ans_right + 1]切片即可
class Solution:
def minWindow(self, s: str, t: str) -> str:
cnt_t = Counter(t)
cnt_s = Counter()
ans_left = -1
ans_right = len(s)
left = 0
for right, x in enumerate(s):
cnt_s[x] += 1
while cnt_s >= cnt_t:
if right - left < ans_right - ans_left:
ans_left, ans_right = left, right
cnt_s[s[left]] -= 1
left += 1
return "" if ans_left < 0 else s[ans_left: ans_right + 1]13.最大子数组和(53)

这道题再次运用到前缀和的思想,我们先对数组求出前缀和数组,然后对前缀和数组进行遍历,如果我们想要找到最大的连续子数组,那么我们要做的只是求出当前位置的前缀和,减去之前位置前缀的最小值,中间的元素就构成了最大和的连续字数组,最终用 ans 进行最大值的记录并输出
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
ans = -inf
min_pre_sum = pre_sum = 0
for x in nums:
pre_sum += x
ans = max(ans, pre_sum - min_pre_sum)
min_pre_sum = min(min_pre_sum, pre_sum)
return ans14.合并数组(56)

这道题的思路是第一步先把给出的数组排序,这里使用到sort 函数的一个特殊用法:sort(key=lambda x:x[0]),意思就是说排序的依据是每个子数组元素中的第一个元素大小,如果是这么排序就可以使得后面的操作方便很多。
排序之后,解题思路主要是对数组元素进行遍历,然后判断如果前一个区间的闭合位置大于目前区间的起始位置,那么就把前一个区间的起始位置和目前区间的闭合位置组成一个区间,也就是将数组进行合并,然后继续向后判断,如果不满足这种情况,说明出现断点无法合并,就推进 ans 里面进行记录
class Solution:
def merge(self, intervals: List[List[int]]) -> List[List[int]]:
if not intervals:
return []
intervals.sort(key=lambda x: x[0])
ans = []
start, end = intervals[0]
for i in range(1, len(intervals)):
current_start, current_end = intervals[i]
if current_start <= end:
end = max(end, current_end)
else:
ans.append([start, end])
start, end = current_start, current_end
ans.append([start, end])
return ans


